It has been generally determined that the universe started out, in the past, much smaller in size thazn it is today. Actual it is the space between things has been increasing with time.
We will be mostly talking about what is called the observable universe, although much of our discussion can be generalized to the total universe. This is because we on earth have a limit to the amount of the universe that we can see. This limit is controlled by the speed that light travels and the amount of time since the light was created. How much of the total universe is observable is an open question and is heatedly debated. We will review this debate in future sections.
Observational Data
First, we will concentrate on the experimental and observational data that has been collected.
The data for how the universe has expanded in the past is mostly based on the red-shift observations of 1a supernovae. Type 1a supernovae are exploding stars that result when enough mass accretes onto a white dwarf to exceed the Chandresekhar limit. When this happens the white dwarf star collapses and expels its outer layer in an extremely bright explosion. Type 1a supernovae are relatively rare and short term phenomenon, but there are enough occurring in the observable universe that it is fairly easy to find one somewhere in the night sky at any given time.
There is some controversy as to whether type 1a supernovae can be used as “standard candles” in determining distance and red shift. As much as this is still being debated, I do not have enough expertise to make an argument for or against this assumption. Therefore, I will assume the astronomers that have taken this data are correct and use their data as it has been reported.
The data on 1a supernovae can be divided into four tranches. The first is data collected prior to 1990 and includes information on supernovae occurring relatively close to the Milky Way Galaxy. The second set of data comes from the High-Z Supernova Search project that was reported in 1998. The third comes from the Supernova Cosmology Project, which also reported its data in 1998. And the final trauche is data from observations that have been made since the year 2000.
The pre-1999 data was visualized quite nicely by Perlmutter, et al in their analysis of their data in Physics Today (2003). A stolen reproduction of their graph is shown in figure 1 below.
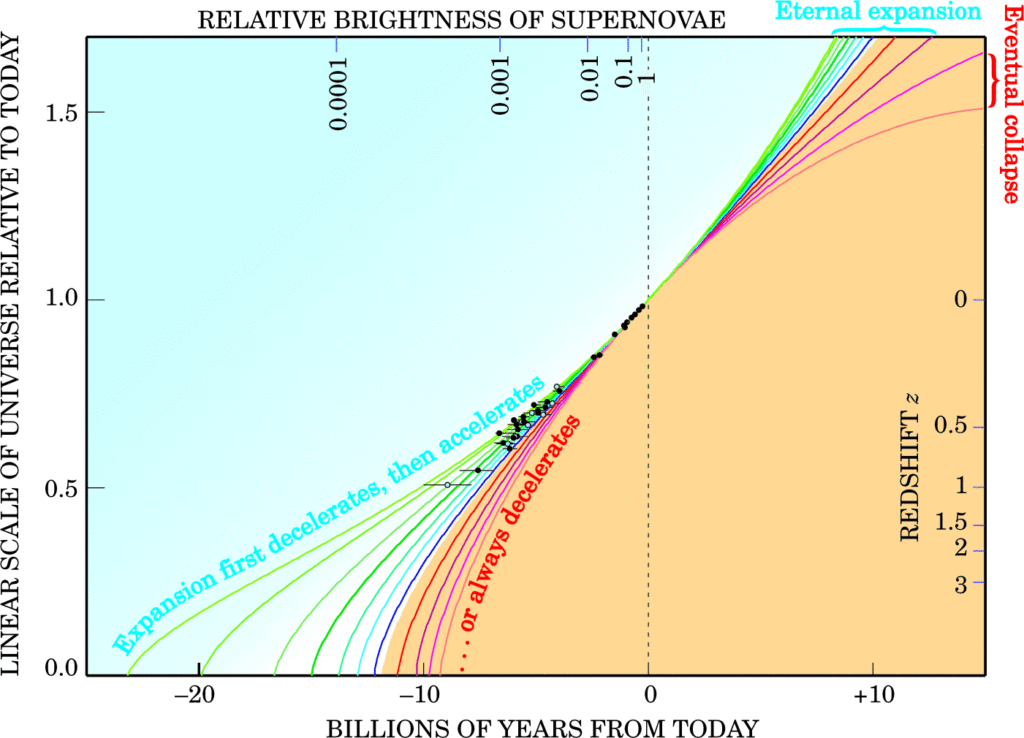
This is a graph of the relative size of one dimension (x,y, or z) of the universe to the value for today (xo) as a function of time from today. The lines on the graph are just speculation about how the size of the universe might be related to time. Some of the lines seem to form complex curves with no apparent reasoning. The area of the graph above the value of 1.0 and to the left of 0 is a representation of what might occur in the future. As much as this might be interesting, it has no bearing on our analysis.
It should be noted that the actual data was gathered as red shift (right axis) and relative brightness (top axis). This data was then translated to relative scale and distance/time, respectively.
Now the data is concentrated in middle of the graph, from 0.5 to 1.0 scale factor and -10 to 0 billion years before today. If we zoom in on this area, and remove the speculative lines, we can get a graph like Figure 2.
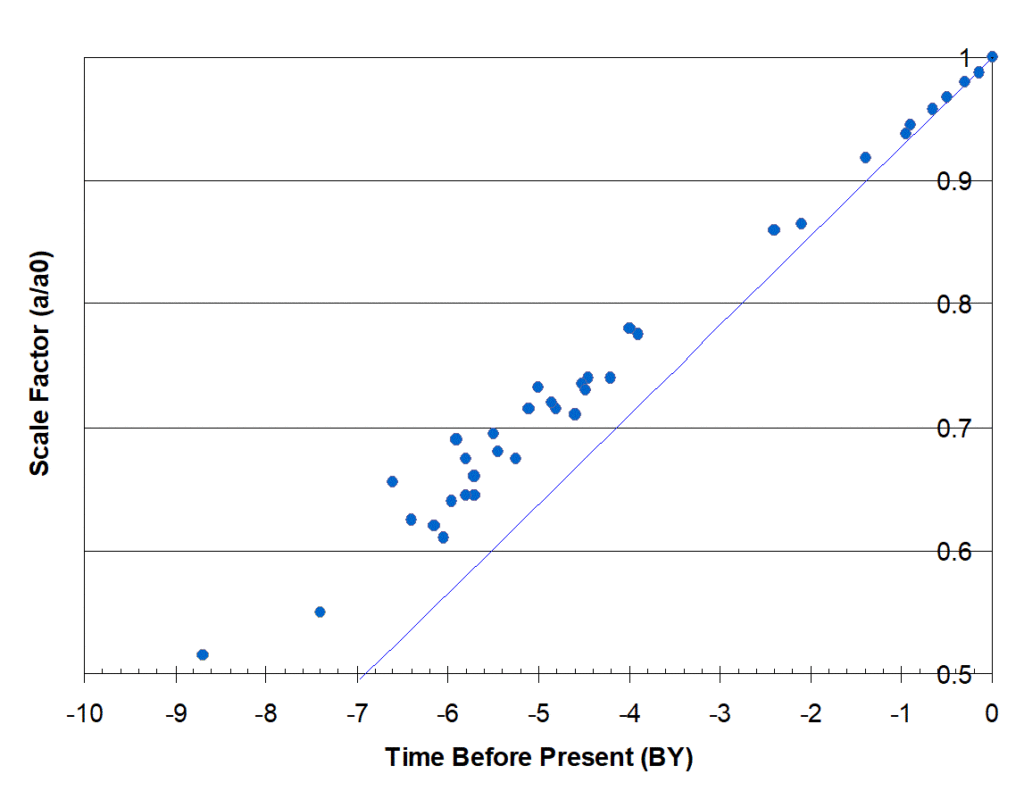
Figure 2. Blow up of central part of Figure 1.
Much of the data that has been determined prior to 1990 and represents supernovae less than 1 billion light-years from the earth has been suppressed to make the graph less cluttered. All of the data were fitted to a straight line from time 0 to time -13.8 billion years and from a scale factor of 1 to 0. The graph shows this straight line in blue. As we can readily see, the data from the High-Z Supernova Search and the Supernova Cosmology Project does not fit this straight line at all.
To curve-fit all of the data, we need to determine what type of curve we are trying to determine. The following possibilities were examined:
- Straight line (monomial)
- Binomial
- Trinomial
- Exponential
- Reciprocal
The straight line, trinomial, and reciprocal regressions had poor curve fits (R2 values < 8). The binomial regression had the best curve fit, followed closely be the exponential. See figure 3 below.
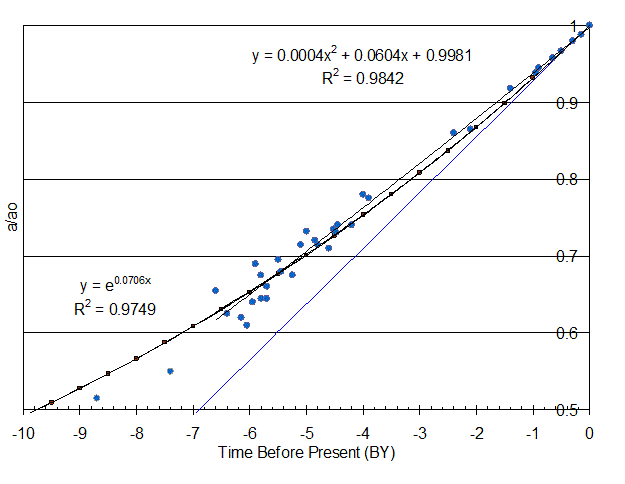
Figure 3. Binomial and Exponential Curves for Type 1a Supernovae Data
The equations are (with time before present as a negative number):
a/a0 = 1 + (4 x 10-22 years-2) t 2 + (6.04 x 10-11 years-1) t
and
a/a0 = e (7.06 e -11 /years) t
Extending a graph beyond its know data points is a dangerous action, but I am going to do that with this data to see whether it can give us information about what might have been happening before the universe was 1/8 the size it is today (about 10 BYA).
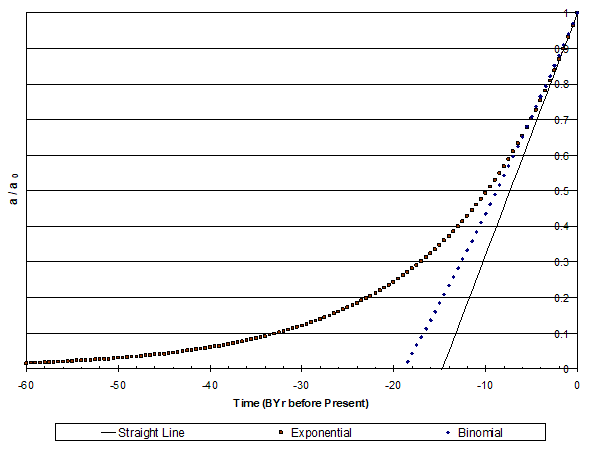
Figure 4. Extension of Curves of Relative Size vs. Time Before Present
The binomial equation gives a nice zero size value of about 19 billion years before present. The exponential equation gets messy, since exponentials never reach zero. However, since we have already assumed that the smallest size of the universe VMIN cannot be zero, this just means that the age of the universe is going to be very large (> 500 billion years), with most of that time occurring during a phase where the universe is physically very small.
There is one other point on this graph that can be determined. That is the size ratio at which the Cosmic Microwave Background Radiation (CMBR) occurs. The CMBR was generated when the kinetic energy density of the universe decreased to the point where the electrons in the universe were not energetic enough to escape from their orbits around protons. This occurs at a point where the temperature drops below 3100 K.
The average cosmic temperature today (where a/a0 = 1.00) is estimated to be 2.73 K. So, if we assume that the amount of kinetic energy has not changed (although in truth is has decreased; but not more than 6-10%), we can calculate that:
VCMBR = ( T0 / TCMBR ) * VCMBR
and since a3 = V: aCMBR /ao = ( 2.73 / 3100 ) 1/3 = 0.096
give or take 0.003
Therefore, we can add this line to the graph. And it should be noted that we have no really good information about what happened before this point, although we can infer what occurred from our knowledge of sub-atomic physics.
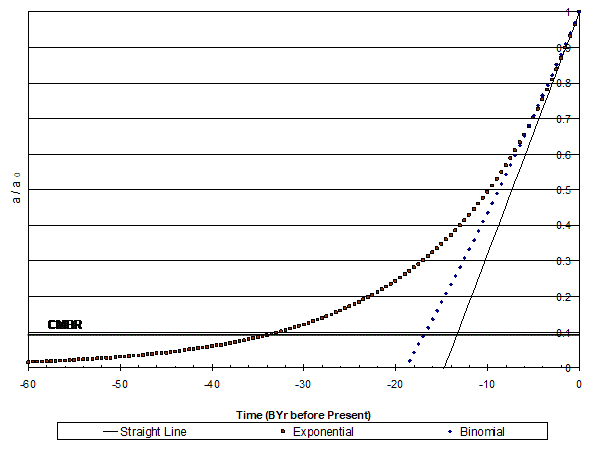
Figure 5. History of the relative size of the universe with the CMBR added.
Inflation
The present Standard Model of the universe assumes that the universe went through a phase of rapid expansion just after it was formed. This phase is referred to as Inflation. Inflation is usually defined as starting with the observable universe somewhere between ½ and 5 million cubic light-years in volume (a/a0 = 1 x 10-9 ), and ending with the observable universe at a volume of 4.25 x 1017 cubic light-years (a/a0 = 1 x 10-5 ). The “Inflationary Epoch” lasted approximately 1 x 10-32 seconds. This would then result in a Hubble Value for this time period of :
HINFLATION ≈ 1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000,000,000,000,000,000,000,000,000,000,000,000,000 km/s/Mpc
The inflation then abruptly stops for some unknown reason. From that time (1/1x 10 32 of a second after the universe formed) until 380,000 years later, the observable universe expands from 4.25 x 1017 ly3 to 2.6 x 1029 ly3. This would be the equivalent of a Hubble Value of:
HPOST INFLATION ≈ 1500 Km/s/Mpc
Then, 380,000 years after the beginning of time, the universe cools to a point where electrons can no longer escape from orbits around protons. This results in the CMBR and the beginning of the universe that we can observe.
Note: This is only a cursory look at Inflation. For a better description of Inflation Theory, check out other cosmology sources.
Whether inflation occurred or not is still an open question in cosmology. We will look at both possibilities (age of universe = time to CMBR + 380,000 years or age of universe = a longer time), for our analyses.
Possible Ages of Universe
This gives us four possible time spans between the beginning of time (tMIN ) and the present time (t0 ).
|
Binomial Model |
Exponential Model | |
|
With Inflation |
17.8 Billion Years |
34.0 Billion Years |
|
Without Inflation |
18.6 Billion Years |
> 800 Billion Years |
The binomial model gives us nice ages that are consistent with the age that cosmologists have been working with using conventional models of the universe. The exponential model with inflation gives an age about twice what most references assume; but it is not out of the question. The exponential model without inflation results in an age of the universe that is way beyond what most Big Bang Theory models find reasonable.
However, I am going to favor the Exponential Model without inflation for analysis. This is for three reasons:
The equation is simpler – there is only one factor to consider
The factor multiplied by the exponential is:
7.06 x 10-11 yr-1 which equals 69 km/s/Mpc = Hubble’s Constant
so the equation can be rewritten as:
a/a0 = e Ho t
Although, the amount of time that the universe exists is extremely large; during the majority of this time the size of the observable universe is very small (less than 1 cubic light-year in volume).
Aside 1: Kinetic Energy Density and Temperature
An important parameter in our discussion is the average kinetic energy density of the universe at given times (expressed in Watts or electron-volts per cubic meter). However, these units are not generally used to describe systems in basic science. Instead we use a proxy characteristic called temperature. Temperature is much easier for people to understand and is related to the total mass of a system and its kinetic energy density. For systems like the universe as a whole, where the total mass is relatively stable, the absolute temperature (expressed in Kelvins) is directly related to the kinetic energy density. For this reason, we will tend to use the absolute temperature value as a substitute for kinetic energy density in our discussions.
Aside 2: Smallest Units
Quantum mechanics defines a limit to how small some values can be. These minimums are generally referred to as Planck values. So, the smallest unit of length is considered to be one Planck length which is 1.6 x 10-35 meters. And therefore the smallest unit of volume is one cubic Planck length or (4.2 x 10-105 m3 ). The shortest length of time is one Planck time which equals approximately 5.4 × 10−44 seconds.
History Part 1 – Standard Model
In the present model of the universe, space comes into existence at time = zero + the smallest increment of time . The amount of space in the observable universe that is created is somewhere between ½ and 5 cubic light-years in volume. Or, in other words, xMIN = yMIN = zMIN = approximately 0.8 to 1.6 light-years.
In the next smallest unit of time, all matter and energy comes into existence. Matter comes into existence as electrons, quarks, tau particles and muons; basically in the ratios that we see today. Energy comes into existence as photons of radiant energy, gluons, w-bosons, and a tiny amount of vacuum energy (about 1/1030 times as much as exists today).
An alternate theory describes a process where about one million times as many particles of matter come into existence alone with one million times as many corresponding anti-particles (positrons, anti-quarks, etc.). These particles then join together to form energy, leaving behind the matter that we see in the universe today:
1 million particles + 1 million anti-particles → 1 particle + 1 mil. energy
This theory allows for the conservation of electro-magnetic charge, spin and color. However, it does not explain where the 1 million times as much energy disappears to, or why 1 million – 1 million = 1.
After all of the matter, energy and space has formed – at about 1 x 10 – 35 second – inflation begins to occur. Over the next 1 billionth of a trillionth of a trillion of a second, the observable universe expands to 2.6 x 1029 cubic light-years. This is about 1/1500th of the size it is today.
Over the next 380,000 years the following transitions occur:
at 10-12 seconds: The Electro-weak Phase Transition – Where the electro-magnetic force decouples from the weak interaction and matter gains its electric charge
at 10-6 seconds: The Quark-Gluon Phase Transition – Where gluons begin to form and then quarks and gluons combine to form protons and neutrons
at 10 seconds: Premordial Nucleosynthesis – Where protons and neutrons begin to combine to form atomic nuclei.
And all of these transitions occur remotely, without interaction between regions of space, since the observable universe is more than 500,000 ly across at the beginning of this period.
Then, 380,000 years after the beginning of time, the kinetic energy density of the universe decreases to a point where electrons are no longer being knocked out of their orbits around protons, and stable atoms form. This process is referred to as Re-combination. These atoms are in the form of monatomic hydrogen, helium, deuterium, and a little bit of tritium and lithium. Since the photons of radiant energy are no longer interacting with the electrons, this phase transition produces a uniform spectrum of light, with a peak radiance at a wavelength of about 4 x 10 -7 meters. This uniform radiant energy results in the CMBR and the beginning of the universe that we can observe.
The extreme uniformity of the CMBR (deviation of less than 1 part in 10,000) must result from an extremely uniform distribution of matter and energy in the universe at this time.
Finally, 500,000 years after the re-combination, the first stars begin to undergo nuclear fusion. Gas clouds, galaxies, and eventually galactic clusters and black holes form. 13.5 billion years after re-combination, we get to the present day.
History Part 2 – Revised Model
An alternative history of the early universe is presented here. It will begin with the presence of matter, with a minimum or no volume of space. The revised history will not include an inflation epoch, but will rely upon longer times to account for the uniformity of the matter and energy in the universe before the CMBR point.
Time starts at t = tMIN , where: x = xMIN , y = yMIN , and z = zMIN ,
and therefore: Volume V = VMIN
Further, MEK equals the sum of: M = total resting mass
E = total radiant energy
and K = total kinetic energy
* MEK is always constant.
However, at t = tMIN : M = MMIN and E = EMIN , so therefore K = KMAX
Or, in other words, we start off the universe (in the past-present-future direction) with the minimum amount of space (volume) to hold the minimum amount of resting mass, the minimum amount of radiant energy and the maximum amount of kinetic energy.
The first question that needs to be answered is:
How can we have a massive amount of kinetic energy without much resting mass and virtually no radiant energy?
By looking at the table of standard particles in the Standard Model, we find that the tiniest particles, Neutrinos, consist of kinetic energy and no (or very little) resting mass.
So, we then can say that all the mass/energy (MEK) in the universe at t = timeMIN has only kinetic energy if it consists entirely of neutrinos.
The estimated total mass in the observable universe is about 1053 kg or 1089 eV, and one neutrino has about 0.8 – 1.0 eV of kinetic energy.
So in the beginning of the universe there were approximately 1.1 x 1089 neutrinos and nothing else. These neutrinos existed in a volume that depends on how closely they can be packed. (If each neutrino occupies one cubic Planck length; then the total volume of the universe would be 1.1 x 1089 x 4.2 x 10-105 m3 = 4.6 x 10-16 m3 . This is about the size of a speck of dust)
At time = tMIN + 1 UNIT the neutrinos begin to vibrate and collide with one another. If the neutrinos are not perfectly elastic, they will then slow down, converting some of the kinetic energy into resting mass and radiant energy. This mass and energy are created at a ratio of 7 parts radiant energy to 3 parts resting mass for some reason. I don’t know why this occurs, but this ratio of energy to mass is found to be consistent for a number of different conversion processes in physics.
The resting mass will then absorb/eliminate space around itself. At the same time the radiant energy creates space around itself. Since there is more radiant energy than resting mass, excess space comes into existence. As space increases, the kinetic energy density (and thus temperature) decreases.
Once the kinetic energy density decreases enough, the neutrinos begin to accumulate together to form masses. This process proceeds for hundreds of billions of years.
When the universe reaches a size that the observable universe has a volume of about 4 x 1016 cubic light-years, and a temperature of 1015 K, the three fundamental forces – electro-magnetism, the weak interaction, and the strong interaction differentiate – and gluons begin to form out of kinetic and radiant energy.
The resting masses that are accumulating form into the other nine types of particles that have been found to be a part of the Standard Model. Actually, only the smallest three of these particles of matter form in any significant numbers:
Electrons made up of 540,000 neutrinos
Up Quarks made up of 3,200,000 neutrinos
Down Quarks made up of 6,400,000 neutrinos
These electrons, up quarks and down quarks have enough kinetic energy to freely flow around the universe in a plasma along with the left-over neutrinos, the gluons, and the radiant energy photons. This phase lasts for about 1 billion years.
Once the excess radiant energy has produced enough new space to drop the kinetic energy density down to a temperature below one trillion K, the quarks and gluons (and possibly some extra neutrinos) combine to form protons and neutrons.
At this point in time the Electro-Magnetic Era of the universe begins, and electro-magnetic charge becomes the dominant force controlling the interactions between particles of matter. Electrons are captured into orbits around protons, but they have enough kinetic energy such that any interaction with photons or other electrons knock them out of orbit and back into space. The neutrons, being charge-neutral, accumulate with themselves and with protons by gravity. This forms light atomic nuclei (deuterium, tritium, helium, and a minute amount of lithium). The protons, however, each have positive charges and repel each other to the greatest extent possible.
After 10 billion years, the protons have spaced themselves out into a very, very even 3-dimensional matrix of particles, immersed in a plasma of fast-moving electrons, photons and neutrinos. The only inconsistencies in this matrix occur where neutrons have attached themselves to individual protons or pairs of neutrons have attached to pairs of protons.
The plasma surrounding the matrix of protons/neutrons is filled with free-flowing electrons, so it would be like a ball of lightning that fills the whole universe. The photons flying around the plasma would create a blinding yellow/white light also filling every cubic inch of the universe.
The photon/mass imbalance would continue to increase the size of the universe, decreasing the mass density, energy density, kinetic energy density and temperature. Once the temperature decreases below 3100 K, the electrons that are captured by the protons no longer have enough kinetic energy to escape, and hydrogen, helium and lithium atoms are formed. Due to the evenness of the proton matrix, this event occurs effectively simultaneously throughout the universe (within 5 – 10 years everywhere).
This point in time is referred to as Combination or Recombination and ends the electro-magnetic dominating era and begins the Atomic Era. The photons of radiant energy are also very consistent at this point in time, since their frequency/wavelength has been regulated by their interactions with the electrons. The spectrum of this light energy is a single range with a maximum intensity at about 400 nm. After this point gravity dominates the interactions between matter particles, although magnetic fields also play a vital part in interactions, particularly at the stellar and galactic scales.
Some people refer to the period after Recombination as the dark age, since stars have not formed yet, and no new light is being created. However, the radiant energy from the electro-magnetic era still exists, and is still shining. So this time period would be anything but dark. A million years after Recombination, you would be seeing Recombination light from 1 million light-years away converging on you from every direction. And, since there is no solid matter to block the light, you would still be blinded. Over the course of billions of years, this radiant energy would be diluted to a lower intensity and will red-shift out of the visible light range, but initially it would be very intense.
Within five to ten billion years from the beginning of the atomic era, stars and galaxies formed through the influence of gravity while the space between galaxies continues to increase due to the effect of the residual radiant energy. The oldest stars that mankind has discovered in the Milky Way Galaxy started nucleosynthesis about 14.5 billion years ago, but stars in other galaxies may be much older.
In the interior of the stars, kinetic energy continues to be converted into resting mass and radiant and binding energies. This results in larger and larger atomic nuclei, which are then eventually expelled from the stars into space. The earth and sun formed from some of this debris.
The atomic era should span a very long period of time. It will end when all of the kinetic energy is converted to resting mass and radiant energy; when all of the radiant energy reaches a maximum wavelength/minimum frequency; and all resting mass has reached maximum density (inside of one or more blackholes). This is sometimes referred as the heat death of the universe, since at this point the temperature of the universe will go to zero.
Reconciling the Observed Cosmic Data with the Theoretical Ideas
Warning: The following section is going to be based on mathematical derivations and, in some cases, contain sophisticated high-level mathematics. However, since I am not much of a mathematician myself, I am going to skate over the really tough stuff.
In an earlier section, we used the data from cosmological observations to determine the following equation:
a / a0 = e Ho t
where, H0 = 7.06 x 10 -11 year -1
However, we are now interested in determining an equation for the rate of expansion. This is: á / a (or the rate of change in one dimension – x, y , or z – as a function of time).
So, we start with: á / a = ( á / a0 ) / ( a / a0 )
where á / a0 is the derivative of a / a0
or á / a0 = d ( e Ho t ) / dt
á / a0 = H 0 e Ho t
so á / a = ( H 0 e Ho t ) / ( e Ho t ) = H0
Which makes sense, since H0 is the Hubble Constant and it is by definition equal to á / a.
H0 ≡ á / a
Now we want to find the a theoretical equation to define á / a0 .
We can start at the beginning, with Albert Einstein’s explanation of how gravity effects the warping (eliminating) of space with time. Originally, Einstein and Georges Lemaître set out to explain how matter affected the four-dimensional space-time continuum. They developed, in concert with several other physicists the following tensor equation; usually referred to as the Einstein Field Equation (EFE):
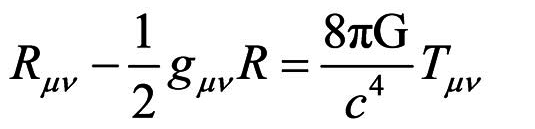
where: Rμν = the Ricci tensor,
gμν = the metric tensor, and
Tμν = the Stress-energy tensor.
Now, a tensor equation is a shorthand way of writing an array of similar equations. In this case the EFE is a four by four matrix of equations to describe the effects of matter traveling in one dimension (time, x-direction, y-direction or z-direction) on the change in size of that dimension or one of the other dimensions. Therefore, there are 16 different equations each of which describes:
The effects of energy/matter moving in the:
|
on the: | time direction | x direction | y direction | z direction |
|
time |
Equation 1 |
Equation 5 |
Equation 9 |
Equation 13 |
|
X |
Equation 2 |
Equation 6 |
Equation 10 |
Equation 14 |
|
Y |
Equation 3 |
Equation 7 |
Equation 11 |
Equation 15 |
|
Z |
Equation 4 |
Equation 8 |
Equation 12 |
Equation 16 |
We can simplify this a bit right away by remembering that we are assuming that the universe is homogeneous and isotropic in space (Basic Axiom #2); which means that many of these equations are equal. We then get the array:
The effects of matter moving in the:
|
on the: | time direction | x direction | y direction | z direction |
|
time |
Equation A |
Equation C |
Equation C |
Equation C |
|
X |
Equation B |
Equation D |
Equation E |
Equation E |
|
Y |
Equation B |
Equation E |
Equation D |
Equation E |
|
Z |
Equation B |
Equation E |
Equation E |
Equation D |
And:
Equation A is the change in time when there is matter moving in time
Equation B is the change in space when there is matter moving in time
Equation C is the change in time when there is matter moving in space
Equation D is the change in one direction when matter is moving in that direction
Equation E is the change in one direction when matter is moving in another direction
The equation we are interested in is Equation B, because we want to know how matter (resting mass) and radiant energy affect the x, y, and z dimension as they exist in the dimension of time.
Fortunately, a very smart mathematician named Alexander Friedmann derived a scalar equation for this aspect of the EFE in 1922. The original Friedmann’s Equation for the contraction of space in one dimension by the presence of matter is:
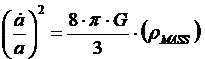
where: G = Newton’s gravitational constant (6.67 x 10-14 m3/g-s2 )
π = pi (3.1415926)
ρMASS = density of total mass in the volume (in g/m3 )
This equation is mathematically rigorous, but it presented a fundamental problem for Albert Einstein. Einstein believed that the universe was infinity and steady-state (it would not change significantly throughout an infinite amount of time), and his equations predicted a universe that would quickly collapse in on itself if it contained any matter. There is no way that Friedmann’s equation can get a contraction equal to zero, if the mass density is any value above zero. Einstein got around this problem by introducing a fudge factor into the equation, which he called the Cosmological Constant (- Λ). This value could then be set equal to the negative of theright side of the equation, and then added to the right side to give an á / a value of zero.
So the Friedmann Equation became:
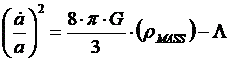
Soon after Einstein and Friedmann published this equation. Edwin Hubble and his team at the Mount Wilson Observatory announced their findings that proved the universe was not in a steady state, but was expanding. This did not negate Einstein’s work on the effects of matter in the universe, but actually gave him a justification for his Cosmological Constant. The constant (Λ) became a characteristic of the beginning of the universe (what would eventually be called the “Big Bang”). Matter simply slowed the expansion rate down.
A simple analogy for this is ballistics, which is a concept well known to physicists. If you shoot a cannonball into the air with a powerful cannon, the cannonball travels upward with a maximum initial velocity (vMAX ) and it increases its distance from the earth (y) with time. As gravity acts on the cannonball, the speed at which it rises (dy) decreases with time, until the rising stops and the cannonball begins to fall back to earth (dy becomes negative).
As a parallel, the universe starts with a volume of zero, or close to zero (aMIN ). Some force causes the volume of the universe to being expanding at an initial rate (ΛMAX ) and it increases its volume (a) with time. As gravity acts on the universe, the speed at which it expands (da) decreases with time, until the expanding stops and the universe begins to contract back to aMIN (da becomes negative).
Conversely, if the cannonball is fired with enough force and vMAX = vCRITICAL (escape velocity), then the cannonball will just reach a point where it goes into orbit around the earth and never decreases its height.
So, by analogy, if ΛMAX = ΛCRITICAL, then the universe will reach a steady state volume, and never contract back to a tiny volume.
And, if a cannonball is fired with enough force for vMAX > vCRITICAL, the altitude of the cannonball will increase indefinitely.
As a parallel, if ΛMAX > ΛCRITICAL, the universe never slows completely and will continue to expand until the end of time.
The key then in determining the ultimate fate of the universe is to find the critical values and compare them to what has happened in the past and present. If the present density of the universe is greater than the critical density, then the universe will end in contraction (sometimes referred to as the Big Crunch). If the present density is equal to the critical density, then the universe will plateau at a steady-state volume. And if the present density is less than the critical density, the universe will continue to expand forever.
The present “Standard Model” for cosmic expansion is based on the Friedmann equation. However, several additions and modifications were made to the equation to take into account energy and other factors that might affect the expansion rate.
A very important note: The Friedmann equation was developed to determine the contraction of one dimension of the space in the universe, not the expansion of this dimension of space. In general, expansion is just the negative of contraction, so mathematically this should not matter. However, the Friedmann equation is for calculating the square of the contraction/expansion parameter. And if you square a negative value you come up with the same number as when you square a positive number. So, if the Friedmann equation is used to determine the expansion rate of the universe, the values on the right side of the equation need to have reversed signs.
For the ΛCDM Model of the universe (present-day Standard Model), the modified Friedmann Equation describing the expansion rate of the universe is:
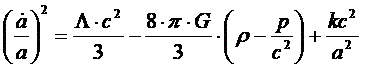
with: á / a = the Hubble value (in sec-1 )
Λ = the cosmological constant (dark energy) (in m-2 )
c = the speed of light in a vacuum ( 300 x 106 m/s)
G = Newton’s gravitational constant ( 6.67 x 10-14 m3 / g-s2 )
ρ = average mass density (in g/m3 )
p = average photon density (in mJ/m3 )
k = shape constant (unitless)
a = diameter of the universe (m)
In general, cosmologists who use the ΛCDM Model assume the shape of the universe is flat and the shape constant (k) therefore equals 0. This eliminates the last factor in the equation. The reason for adding the c2 /3 value to the Λ factor is confusing at best. Λ is a constant and c2 /3 is a constant. It just changes the units on Λ, but we will include these extra values for completeness.
For our initial analysis, we will assume k = 0; although later we will examine what the effect of the shape factor has on the expansion rate if the universe is round.
Cosmologist have estimated that at the present time (t0 ):
average (baryonic) mass density of the universe is 0.20 – 0.25 atoms of hydrogen per m3 , or 3.5 x 10-25 g/m3
average (baryonic) energy density of the universe is about 5 mJ/m3
the Hubble parameter is around 69 km/s/Mpc which equals 2.24 x 10-18 sec-1
the total (baryonic) mass in the observable universe = M = ρMASS x Volume = 3.5 x 10-25 g/m3 x 1.4 x 1080 m3 = 4.9 x 1055 g . (Note: this is for a 34 BY old universe)
We are using baryonic (normal) mass in our analysis because it has yet to be determined if cold dark matter effects the expansion rate of the universe – or even what cold dark matter is. We are using baryonic (radiant) energy in our equation because the Λ value already includes the effect of dark energy.
Plugging these values into the Friedmann equation, gives:
Λ = 1.67 x 10-52 m2
The values of ρ and p will change with time since the volume of the universe is constantly changing, but the ratio p / ρ will not change. The ratio of p / c2 to ρ will constantly equal 2.33. Therefore, the density value in the middle of the equation can be rewritten as:
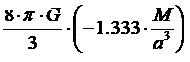
and constant values can be substituted into the equation to get:
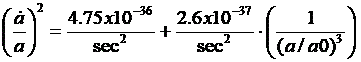
With a in meters.
a0 for the observable universe has already been determined to be 6 x 10 26 m, so we can relate this equation to values for a/a0 . First, to look at how the Hubble parameter will change with decreasing volume we can plot the values of H as a function of a/a0 .
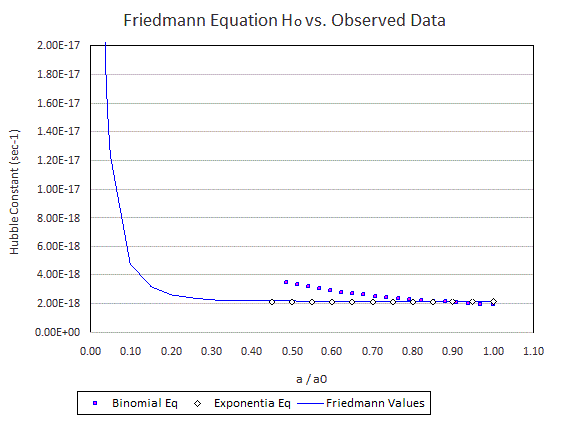
Figure 6.
As can be seen from the graph, the Friedmann Hubble parameter remains fairly constant at 2.35 x 10-18 s-1 throughout the range that astronomers have been able to observe. However, when the volume of the universe decreases below 1/200th of the present volume, the Hubble parameter calculated by the Friedmann equation increases rapidly. This means that we need to go back to the beginning of our analyses and re-graph the a/a0 values vs. time before present, taking into account the fact that H is now not constant.
Observational Data – Part Two
We can now re-plot Figure 4, with a variable value for the Hubble parameter.
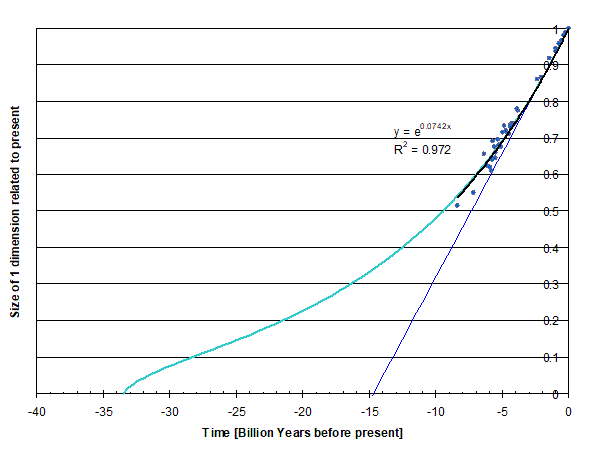
Figure 7. Updated version of Figure 4 to Make it compatible with the Friedmann Equation.
In Figure 7 we can see that the densities of mass and energy have significant effect on the Hubble parameter for times more than 15 billion years before the present. But these do not factor much in the equation for the Hubble parameter today, or on the equation in the future. For this reason, we can refer to H as the Hubble Constant (at least as it relates to time).
This brings us to the next topic of discussion:
Non-homogeneity of the Present Universe
All of these analyses have assumed a homogeneous distribution of energy and matter throughout the space in the observable universe. Whereas radiant energy (particularly the energy created before the re-combination) is uniformly distributed; the same can definitely not be said for resting mass. All discussions of the Standard Model that I have ever encountered ignore this fact.
To include this “lumpiness” in our discussion, we need to divide the universe into three general categories of space:
- Energy dominated space
- Balanced Mass-Energy space
In the Mass dominated space, there is more resting mass present than radiant energy (accounting for e = mc2 ). This is very rare, and only occurs close to and inside black holes. In these spaces, the Hubble parameter is negative and the amount of space is actually contracting. Many cosmologists are presently studying and developing models for these spaces.
The Energy dominated spaces consists of the spaces between galaxies and galactic clusters. This makes up 99.99% of the volume of the observable universe. In these spaces the mass density is significantly less that 0.25 atoms of hydrogen per cubic meter (more like 0.00025). This results in a maximum positive value for the Hubble Parameter. But not much is happening in these volumes. Radiant energy that passes through this space is increasing its wavelength (decreasing its frequency) and this effect is expanding the volume of the space, but that is about it. – Note: leftover neutrinos are also flying through this space, but they don’t really affect anything else as they travel.
The Balanced Mass-Energy spaces are where thing get really interesting. These spaces make up a small part of the volume of the universe, but contain the largest amount of resting mass and kinetic energy today. They also contain us.
In the Balanced Mass-Energy domain, the Hubble parameter is much smaller than 2.25 x 10-18 s-1 (69 km/s/Mpc). In fact, in most of the balanced spaces it is effectively equal to zero This means that overall space is not being either created or destroyed. . The value for H in the region between the earth and other stars in the Milky Way Galaxy can be measured from our knowledge of the space and red shift between us. This balance results in objects orbiting one another on the galactic/planetary scale, and solids and liquids forming stable substances on smaller scales. It is also responsible for the reality that we refer to as chemistry, planetary geology, nucleogenesis, and solid-state physics. The ramifications of the balanced mass-energy space (BMES) will be explored in future essays.
— Brian W. Nelson (8/19/2021)
edited for typos 8/28/2022